Tahukah Anda ? Sejarah Phytagoras dan Macam macam bilangan Phytagoras

Selamat Pagi ,Sekarang saya akan menshare mengenai sejarah,rumus,dan apa sajakah bilangan bilangan phytagoras ,mungking Kata phytagoras itu sudah tidak asing lagi bagi anda sejak SD sampe SMA bahkan kuliah kalian tetap akan mempelajarinya mungkin ada yang sampe bosan dan ada yang mengantuk Saat mendengarkannya #curhat#.

SEJARAH TEOREMA PHYTAGORAS

 Teorema Phytagoras pertama kali di ciptakan Oleh seorang Ilmuan yang bernama Phytagoras juga.Pythagoras (570 SM – 495 SM, bahasa Yunani: Πυθαγόρας) adalah seorang matematikawan dan filsuf Yunani yang paling dikenal melalui teoremanya.

Dikenal sebagai "Bapak Bilangan", dia memberikan sumbangan yang penting terhadap filsafat dan ajaran keagamaan pada akhir abad ke-6 SM. Kehidupan dan ajarannya tidak begitu jelas akibat banyaknya legenda dan kisah-kisah buatan mengenai dirinya.

Salah satu peninggalan Pythagoras yang terkenal adalah teorema Pythagoras, yang menyatakan bahwa kuadrat hipotenusa dari suatu segitiga siku-siku adalah sama dengan jumlah kuadrat dari kaki-kakinya (sisi-sisi siku-sikunya). Walaupun fakta di dalam teorema ini telah banyak diketahui sebelum lahirnya Pythagoras, namun teorema ini dikreditkan kepada Pythagoras karena ia yang pertama kali membuktikan pengamatan ini secara matematis




Pythagoras dan murid-muridnya percaya bahwa segala sesuatu di dunia ini berhubungan dengan matematika, dan merasa bahwa segalanya dapat diprediksikan dan diukur dalam siklus beritme. Ia percaya keindahan matematika disebabkan segala fenomena alam dapat dinyatakan dalam bilangan-bilangan atau perbandingan bilangan. Terdapat legenda yang menyatakan bahwa ketika muridnya
Hippasus menemukan bahwa , hipotenusa dari segitiga siku-siku sama kaki dengan sisi siku-siku masing-masing 1, adalah bilangan irasional, murid-murid Pythagoras lainnya memutuskan untuk membunuhnya karena tidak dapat membantah bukti yang diajukan Hippasus.

RUMUS PERHITUNGAN PHTAGORAS

"Triple pythagoras adalah adalah 3 (tiga) bilangan asli yang memenuhi rumus teorema pythagoras. Rumus teorema pythagoras yaitu c2 = a2 + b2."
NB :PHYTAGORAS HANYA BERLAKU UNTUK SEGITIGA SIKU SIKU













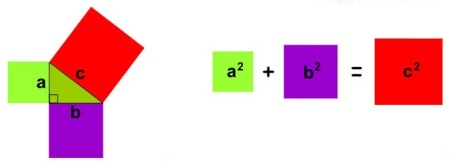
Jika terdapat segitiga yang sisi-sisinya berukuran a, b, dan c maka segitiga tersebut adalah segitiga siku-siku,Setiap sisi dari Phytagoras yang dikuadrat kan sama dengan luas dari sebuah persegi dimana juga dapat dihitung dengan rumus SISI KUADRAT

Macam-macam Tipe Triple Pythagoras

Triple pythagoras ini masih mempunyai 4 bilangan yang susunan bilangannya teratur dan membentuk pola tertentu atau sering disebut sebagai 4 tipe triple pythagoras. :

Judul di atas sepertinya kontras. Matematika mestinya tidak menghafal. Matematika itu ilmu hitung yang tidak perlu dihafal. Kerangka berfikir dalam pelajaran matematika adalah penalaran. Mengedepankan logika.

Contoh Soal Rumus Pythagoras Segitiga

Contoh Soal 1

Diketahui sebuah segitiga memiliki sisi tegak sepanjang 8cm sementara alasnya berukuran 6cm. Kedua sisi tersebut membentuk sudut siku-siku. Tentukanlah panjang sudut miring yang berada tepat dihadapan sudut siku-siku tersebut!

Penyelesaian:

                                                Kuadrat sisi miring = Jumlah Kuadrat sisi siku-siku      

Sisi miring² = sisi tegak² + alas²                                              

Sisi miring² = 8² + 6²

Sisi miring² = 64 cm + 36 cm

Sisi miring² = 100 cm

Sisi miring = √100 cm

Sisi miring = 10 cm

Maka sisi miring pada segitiga tersebut adalah 10 cm

Contoh Soal 2

Sebuah segitiga siku-siku diketahui memiliki panjang sisi miring sebesar 35 cm, panjang alas dari segitiga tersebut adalah 28 cm. Hitunglah luas dari segitiga tersebut!

Penyelesaian:

Untuk mencari luas segitiga kita harus mengetahui tingginya.

Untuk mencari tinggi pada segitiga tersebut kita gunakan rumus pythagoras:

Sisi miring² = sisi tegak² + alas²

Karena t = sisi tegak

Maka rumusnya berubah menjadi:

t² = sisi miring² - alas²

t² = 35² - 28²

t² = 1225 - 784

t² = 441

t = √441 cm

t = 21 cm

Setelah mengetahui tinggi dari segitiga tersebut, barulah kita bisa mencari luasnya:

Luas Segitiga = ½ x alas x tinggi

Luas Segitiga = ½ x 28 x 21

Luas Segitiga = ½ x 588

Luas Segitiga = 294 cm²

DAFTAR BILANGAN PHYTAGORAS

 Berikut daftar bilangan bilangan teorema phytagoras:

1. (3,4,5)

2. (5,12,13)

3. (7,24,25)

4. (8,15,17)

5. (9,40,41)

6. (11,60,61)

7. (12,35,37)

8. (13,84,85)

9. (15,112,113)

10. (16,63,65)

11. (17,144,145)

12. (19,180,181)

13. (20,21,29)

14. (20,99,101)

15. (21,220,221)

16. (23,264,265)

17. (24,143,145)

18. (25,312,313)

19. (27,364,365)

20. (28,45,53)

21. (28,195,197)

22. (29,420,421)

23. (31,480,481)

24. (32,255,257)

25. (33,56,65)

26. (33,544,545)

27. (35,612,613)

28. (36,77,85)

29. (36,323,325)

30. (37,684,685)

31. (39,80,89)

32. (39,760,761)

33. (40,399,401)

34. (41,840,841)

35. (43,924,925)

36. (44,117,125)

37. (44,483,485)

38. (48,55,73)

39. (48,575,577)

40. (51,140,149)

41. (52,165,173)

42. (52,675,677)

43. (56,783,785)

44. (57,176,185)

45. (60,91,109)

46. (60,221,229)

47. (60,899,901)

48. (65,72,97)

49. (68,285,293)

50. (69,260,269)

51. (75,308,317)

52. (76,357,365)

53. (84,187,205)

54. (84,437,445)

55. (85,132,157)

56. (87,416,425)

57. (88,105,137)

58. (92,525,533)

59. (93,476,485)

60. (95,168,193)

61. (96,247,265)

62. (100,621,629)

63. (104,153,185)

64. (105,208,233)

65. (105,608,617)

66. (108,725,733)

67. (111,680,689)

68. (115,252,277)

69. (116,837,845)

70. (119,120,169)

71. (120,209,241)

72. (120,391,409)

73. (123,836,845)

74. (124,957,965)

75. (129,920,929)

76. (132,475,493)

77. (133,156,205)

78. (135,352,377)

79. (136,273,305)

80. (140,171,221)

81. (145,408,433)

82. (152,345,377)

83. (155,468,493)

84. (156,667,685)

85. (160,231,281)

86. (161,240,289)

87. (165,532,557)

88. (168,425,457)

89. (168,775,793)

90. (175,288,337)

91. (180,299,349)

92. (184,513,545)

93. (185,672,697)

94. (189,340,389)

95. (195,748,773)

96. (200,609,641)

97. (203,396,445)

98. (204,253,325)

99. (205,828,853)

100. (207,224,305)

101. (215,912,937)

102. (216,713,745)

103. (217,456,505)

104. (220,459,509)

105. (225,272,353)

106. (228,325,397)

107. (231,520,569)

108. (232,825,857)

109. (240,551,601)

110. (248,945,977)

111. (252,275,373)

112. (259,660,709)

113. (260,651,701)

114. (261,380,461)

115. (273,736,785)

116. (276,493,565)

117. (279,440,521)

118. (280,351,449)

119. (280,759,809)

120. (287,816,865)

121. (297,304,425)

122. (300,589,661)

123. (301,900,949)

124. (308,435,533)

125. (315,572,653)

126. (319,360,481)

127. (333,644,725)

128. (336,377,505)

129. (336,527,625)

130. (341,420,541)

131. (348,805,877)

132. (364,627,725)

133. (368,465,593)

134. (369,800,881)

135. (372,925,997)

136. (385,552,673)

137. (387,884,965)

138. (396,403,565)

139. (400,561,689)

140. (407,624,745)

141. (420,851,949)

142. (429,460,629)

143. (429,700,821)

144. (432,665,793)

145. (451,780,901)

146. (455,528,697)

147. (464,777,905)

148. (468,595,757)

149. (473,864,985)

150. (481,600,769)

151. (504,703,865)

152. (533,756,925)

153. (540,629,829)

154. (555,572,797)

155. (580,741,941)

156. (615,728,953)

157. (616,663,905)

158. (6,8,10)

sekian Postingan saya hari ini,

Tq

Sumber : 

http://irwant-suttisna.blogspot.co.id/2013/10/macam-macam-bilangan-tripel-pythagoras.html

https://id.wikipedia.org/wiki/Pythagoras